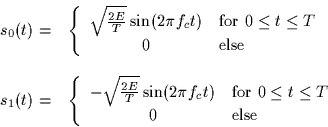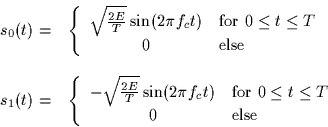Next: Gaussian Pulses
Up: Collected Problems
Previous: Suboptimum Receivers
The following binary signal set is used to transmit equally likely
messages over an additive white Gaussian noise channel (spectral
height 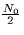 ),
),
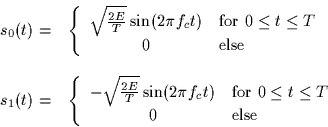
- 1.
- Draw a block diagram of the optimum receiver
which uses only a single correlator.
- 2.
- Compute the
probability of error for this receiver.
- 3.
- Assume now that the local oscillator at the receiver is not in-phase
with the received signal.
In other words, the receiver correlates with
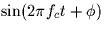 instead of
instead of 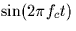 .Find the probability of error as a function of the phase error
.Find the probability of error as a function of the phase error 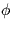 .
. - 4.
- Compute the probability of error for the case
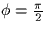 and illustrate this case in a suitably chosen signal space.
and illustrate this case in a suitably chosen signal space.
Hint: 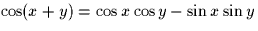 .
.
Prof. Bernd-Peter Paris
3/3/1998