


Next: 2-Bit Adder
Up: Combinatorial Logic: Binary AdderNovember
Previous: 1-Bit Adder (Half Adder)
- When two (or more) bit binary numbers are added, the problem is somewhat
more complicated.
- Example: Add binary representations of 3 (11) and 1 (01).
| |
1 |
1 |
(3) |
| + |
0 |
1 |
(1) |
| 1 |
1 |
|
(carry) |
| 1 |
0 |
0 |
(result) |
- The example illustrates that for all but the rightmost bit, not two but
three bits must be added.
- The carry bit from the previous bit addition must be reflected.
- The truth table for the full adder (with carry input) is
| A1 |
B1 |
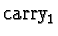 |
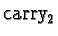 |
S1 |
| 0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
1 |
| 0 |
1 |
0 |
0 |
1 |
| 0 |
1 |
1 |
1 |
0 |
| 1 |
0 |
0 |
0 |
1 |
| 1 |
0 |
1 |
1 |
0 |
| 1 |
1 |
0 |
1 |
0 |
| 1 |
1 |
1 |
1 |
1 |
- The carry bit
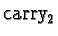 is 1 if
is 1 if
- both A1 and B1 are 1, or
- exactly one of A1 and B1 is 1 and the input carry,
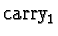 ,
is 1.
,
is 1.
- The sum bit S1 is 1 if an odd number of the three inputs is on, i.e.,
S1 is the XOR of the three inputs.
- Hence, the full adder can be realized as shown below.
- Notice that the full adder can be constructed from two half adders and an
OR gate.



Next: 2-Bit Adder
Up: Combinatorial Logic: Binary AdderNovember
Previous: 1-Bit Adder (Half Adder)
Prof. Bernd-Peter Paris
1998-12-14
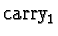 ,
is 1.
,
is 1.