


Next: Modulation
Up: Collected Problems
Previous: Collected Problems
Assume the impulse response of a channel is given by
The amplitude of the delayed component is constant.
- Is the channel time-varying or time-invariant. Explain.
- Find the response of the channel if the following signals are applied as
the input to the channel
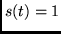 for all
for all  ,
,
-
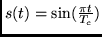 for all
for all 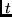 ,
,
-
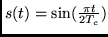 for all
for all 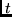 .
.
- Find a general expression for the response of the channel, when the input
is
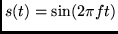 for all
for all 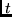 .
.
- Plot the magnitude of the response as a function of the frequency
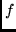 .
.
- What conclusions you can draw from that plot?
- Express the coherence-bandwidth of the channel in
terms of the parameters.
- The above channel is used to transmit digitally modulated data at a rate
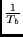 . Data are transmitted in packets of
. Data are transmitted in packets of 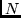 symbols. For each of
the following cases indicate if the channel is frequency selective or
non-selective.
symbols. For each of
the following cases indicate if the channel is frequency selective or
non-selective.
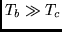 ,
,
-
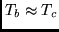 .
.
- For each of the two cases, explain which provisions must be made to
ensure reliable communication.



Next: Modulation
Up: Collected Problems
Previous: Collected Problems
Dr. Bernd-Peter Paris
2003-12-08