A more realistic model for the RACH is as follows. A single transmission
is successful with probability 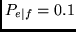 (transmission errors), while one message
is successfully received when two messages are transmitted with probability
(transmission errors), while one message
is successfully received when two messages are transmitted with probability
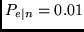 . When all three users transmit in the same time slot, one of the three
messages will be received correctly by the base station with probability
. When all three users transmit in the same time slot, one of the three
messages will be received correctly by the base station with probability
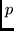 . The non-zero probabilities in the latter two cases are due to a
phenomenon called capture.
. The non-zero probabilities in the latter two cases are due to a
phenomenon called capture.
If 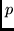 , what is the expected number of time slots until all users have
successfully accessed the RACH?
, what is the expected number of time slots until all users have
successfully accessed the RACH?
![]() , what is the expected number of time slots until all users have
successfully accessed the RACH?
, what is the expected number of time slots until all users have
successfully accessed the RACH?
![]() , what is the expected number of time slots until all users have
successfully accessed the RACH?
, what is the expected number of time slots until all users have
successfully accessed the RACH?