


Next: Coding and Interleaving
Up: Collected Problems
Previous: Collected Problems
Consider a rate 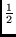 convolutional coder with constraint length
convolutional coder with constraint length 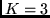 and generator polynomials in octal representation
and generator polynomials in octal representation 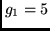 and
and 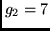 .
.
- Draw a block diagram of this encoder and label it accurately.
- Determine the output from the encoder if the input sequence is
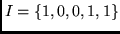 . Assume that the register is initially loaded with
. Assume that the register is initially loaded with
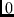 -bits and that
-bits and that 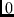 -bits are transmitted after the sequence
as stop bits .
-bits are transmitted after the sequence
as stop bits .
- Assume now that the sequence
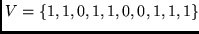 is
received. Again
is
received. Again 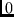 -start and stop bits have been added to the sequence to
force the encoder into the all
-start and stop bits have been added to the sequence to
force the encoder into the all 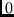 -state at the beginning and end of the
transmission. Thus, there are three information bits between the start and
stop bits.
-state at the beginning and end of the
transmission. Thus, there are three information bits between the start and
stop bits.
Draw a trellis diagram, showing clearly the possible states of the encoder,
the possible transitions and the encoder outputs associated with the
transitions.
- Determine the most likely input sequence.
Dr. Bernd-Peter Paris
2003-12-08
![]() convolutional coder with constraint length
convolutional coder with constraint length ![]() and generator polynomials in octal representation
and generator polynomials in octal representation ![]() and
and ![]() .
.