


Next: Undecided Receivers
Up: Collected Problems
Previous: Pulse Position Modulation
Throughout this problem consider the following two signals
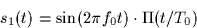
and
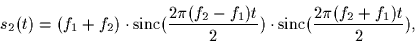
where 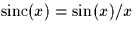 and
and 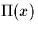 denotes the rectangular
pulse defined in class, i.e.,
denotes the rectangular
pulse defined in class, i.e.,
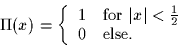
- 1.
- Show that the inverse Fourier transform of
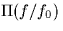 is
given by
is
given by 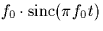 .
. - 2.
- Compute the Fourier transform of s1(t).
- 3.
- Using the convolution rule, find the Fourier transform S2(f)
of s2(t).
Plot the magnitude of S2(f).
- 4.
- Is it possible to completely reconstruct either of the two signals
s1(t) and s2(t) from samples taken at rate 1/Ts?
Justify your answer for each signal separately.
- 5.
- If you answered ``yes'' for either or both of the two signals,
give the largest sampling period Ts
which allows for perfect reconstruction.
Prof. Bernd-Peter Paris
3/3/1998
![]()
![]()
![]()