


Next: Binary Signal Sets
Up: Collected Problems
Previous: Modulation
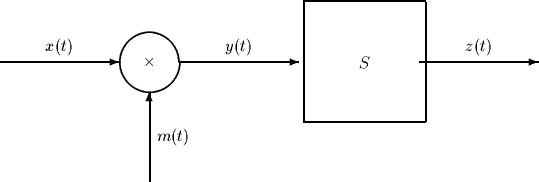
Consider the following system, in which S denotes a linear system to be
determined below and the signal m(t) is given by
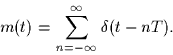
The input signal x(t) is a band-pass signal, i.e.,
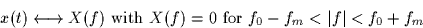
for some f0 and fm.
- 1.
- Sketch the signal m(t) and then show that m(t) can be expanded into
the Fourier series
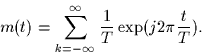
- 2.
- Using the result from part (a), compute the Fourier transform Y(f) of
the signal y(t) in terms of the Fourier transform X(f) of the input signal.
- 3.
- Assume that X(f) is given by

and that the sampling rate 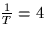 . Sketch and accurately label the Fourier transform Y(f).
. Sketch and accurately label the Fourier transform Y(f).
- 4.
- Is it possible to reconstruct the original signal x(t) from the sampled
signal y(t)? If yes, determine the linear system S that will recover the
signal x(t). If no, explain why not.
- 5.
- Are there any other values for the sampling rate
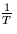 that would
allow reconstruction of x(t) from the sampled signal y(t). Justify your answer!
that would
allow reconstruction of x(t) from the sampled signal y(t). Justify your answer!
Prof. Bernd-Peter Paris
3/3/1998
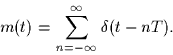
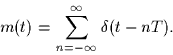
![]()
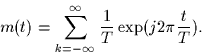
![]()