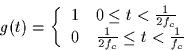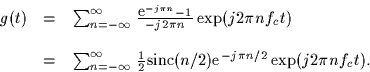Amplitude Modulation

Consider the following amplitude modulated signal,

$$x(t) = (A + m(t)) \cdot \sin(2\pi f_ct).$$

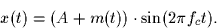
The constant A has been chosen such that (A+m(t))>0 for all t. Furthermore, the spectrum of the message signal m(t) is

$$M(f) = \Pi(f/2f_m) = \left\{ \begin{array} {cl} 1 & \mbox{for $\vert f\vert < f_m$} \\ 0 & \mbox{otherwise.}\end{array}\right.$$

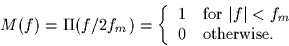
The carrier frequency f_c is much larger than f_m.

To demodulate x(t) we use the following system:

where the signal g(t) is given by:

$$g(t) = \left\{ \begin{array} {cl} 1 & 0 \leq t < \frac{1}{2f_c} \\ 0 & \frac{1}{2f_c} \leq t < \frac{1}{f_c}\end{array}\right.$$

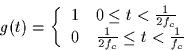
and g(t) is periodic with period 1/f_c, i.e., g(t) = g(t+1/f_c).

1.

Sketch the spectrum X(f) of the signal x(t).

2.

Show that the signal g(t) can be represented as a Fourier series by

$$\begin{array} {ccl} g(t) & = & \sum_{n=-\infty}^{\infty} \fr... ...c}(n/2)\mbox{e}^{-j \pi n/2} \exp(j 2 \pi n f_c t) .\end{array}$$

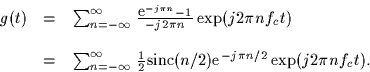
3.

Give an expression for the spectrum G(f) of g(t) and sketch G(f).

4.

Using the results from parts (b) and (c), sketch and accurately label the spectrum Y(f) of the signal y(t) = x(t)g(t).

5.

How would you choose the cut-off frequency of the ideal lowpass, in order to recover the message signal m(t)?