Amplitude modulation with square-waves

Let s(t) be a square-wave signal such that

$$s(t) = \left\{ \begin{array} {cc} 1 & \mbox{for $-\frac{T... ...\frac{T_c}{4} < t \leq \frac{3 T_c}{4}$}.\\ \end{array}\right.$$

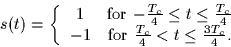
The signal s(t) is used to amplitude modulate a message signal m(t) such that the transmitted signal x(t) is given by:

$$x(t) = (A+m(t)) \cdot s(t).$$

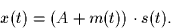
The constant A is chosen to satisfy A+m(t) > 0 for all t.

1.

Assume that the message signal m(t) is a triangular wave with period T=1 and assume further, for this part only, that the period of the square wave 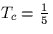$T_c=\frac{1}{5}$. Sketch and accurately label the transmitted signal x(t) under these assumptions.

2.

Compute the Fourier series for the square wave signal s(t). (If you are unable to to solve this part of the problem you may assume that the Fourier series coefficients are given by S₀=0 and 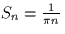$S_n = \frac{1}{\pi n}$ for |n|>0 for the remainder of this problem.)

3.

Assume now that the message signal m(t) is strictly band-limited, i.e., M(f)=0 for |f|>f_m and that 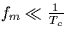$f_m \ll \frac{1}{T_c}$. Using the result from part (b), compute the Fourier transform X(f) of the transmitted signal. Sketch and accurately label the magnitude of X(f) for a ``typical'' message spectrum M(f).

4.

The signal x(t) is now passed through an ideal full-wave rectifier, i.e., a device that computes the absolute value of its input. Determine the output of the rectifier. Show your reasoning!