


Up: Collected Problems
Previous: Sub-Optimum Receivers
The following signal set is used to
transmit equally likely messages over an additive white Gaussian
noise channel with spectral height 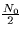 ,
,
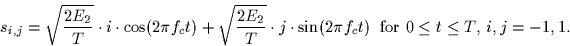
Thus the signal set consists of M=4 signals.
- 1.
- Draw and accurately label the signal constellation in an
appropriately chosen signal space and indicate the decision
boundaries formed by the optimum receiver.
- 2.
- Compute the probability of error achieved by the optimum
receiver.
- 3.
- Determine the number of bits Nb that is transmitted simultaneously
with this signa set.
- 4.
- Define the average bit-energy Eb as
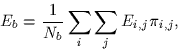
where Ei,j denotes the energy of signal si,j and
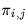 denotes the corresponding a priori probabilities.
Compute the average bit-energy Eb for this signal set.
denotes the corresponding a priori probabilities.
Compute the average bit-energy Eb for this signal set.
- 5.
- Repeat parts (a)-(c) for the following signal set with M=16 signals:
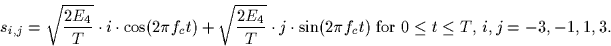
- 6.
- If both signal sets would be using the same bit-energy Eb, which signal set
yields the smaller probability of error? Explain.
Prof. Bernd-Peter Paris
3/3/1998
![]()
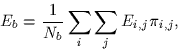
![]()