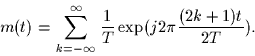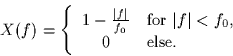Scrambling Device

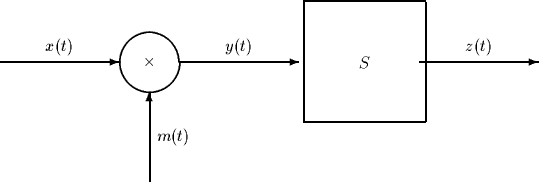
Consider the following system, in which S denotes an ideal lowpass with cut-off frequency 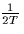$\frac{1}{2T}$ and the signal m(t) is given by

$$m(t) = \sum_{n=-\infty}^{\infty} [\delta(t-2nT) - \delta(t-(2n+1)T)].$$

The input signal x(t) is bandlimited, i.e.,

$$x(t) \longleftrightarrow X(f) = 0 \;\;\;\mbox{for $\vert f\vert \gt f_0$}.$$

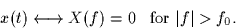
1.

(10 pts) Sketch the signal m(t) and then show that m(t) can be expanded into the Fourier series

$$m(t) = \sum_{k=-\infty}^{\infty} \frac{1}{T} \exp(j 2 \pi \frac{(2k+1)t}{2T}).$$

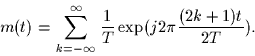
2.

(10 pts) Using the result from part (a), compute the Fourier transform Y(f) of the signal y(t) in terms of the Fourier transform X(f) of the input signal.

3.

(5 pts) Assume that X(f) is given by

$$X(f) = \left\{ \begin{array} {cl} 1 - \frac{\vert f\vert}{... ...vert f\vert < f_0$,}\\ 0 & \mbox{else.} \end{array} \right.$$

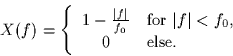
Sketch and accurately label the Fourier transform Y(f).

4.

(5 pts) What condition does the frequency f₀ have to satisfy that no overlapping of partial spectra occurs.

5.

(5 pts) Assuming the condition found in part (d) is met, sketch the Fourier transform Z(f) of the output of the lowpass filter S and describe how the above system scrambles the input signal.