


Next: Mismatched Filters
Up: Collected Problems
Previous: Problem 37
Consider the system in the block diagram below.
- 1.
- Determine the Fourier transforms X1(f) and X2(f) of
the signals x1(t) and x2(t) as a function of the Fourier
transform V(f) of the input signal v(t).
- 2.
- Find the Fourier transforms of the signals Z1(f) and Z2(f)
of the signals z1(t) and z2(t) as a function V(f) and H(f).
- 3.
- Which value of the angle
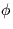 allows W(f), the Fourier transform
of w(t), to be written as
allows W(f), the Fourier transform
of w(t), to be written as
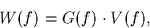
where G(f) is not a function of V(f)?
Express G(f) as a function of H(f) and f0.
- 4.
- Assume now that H(f) is the transfer function of an ideal lowpass
with cut-off frequency
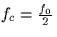 . Sketch |G(f)| for this case.
. Sketch |G(f)| for this case.
Hint: You may need the following identities:
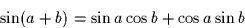
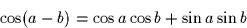
Prof. Bernd-Peter Paris
3/3/1998
![\begin{picture}
(440,200)(80,620)
\setlength {\unitlength}{0.0125in}
%
\thick...
...akebox(0,0)[lb]{$z_2(t)$}}
\put(500,730){\makebox(0,0)[lb]{$w(t)$}}\end{picture}](img42.gif)
![\begin{picture}
(440,200)(80,620)
\setlength {\unitlength}{0.0125in}
%
\thick...
...akebox(0,0)[lb]{$z_2(t)$}}
\put(500,730){\makebox(0,0)[lb]{$w(t)$}}\end{picture}](img42.gif)
![]()
![]()
![]()