M-ary Signal Sets

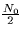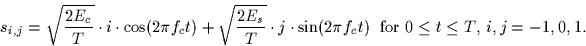
The following signal set is used to transmit equally likely messages over an additive white Gaussian noise channel with spectral height $\frac{N_0}{2}$,

$$s_{i,j} = \sqrt{\frac{2E_c}{T}}\cdot i \cdot \cos(2\pi f_c t... ...(2\pi f_c t) \;\;\mbox{for $0 \leq t \leq T$, $i,j=-1,0,1$.}$$

Thus, this signal set consists of M=9 signals.

1.

Draw and accurately label the signal constellation in an appropriately chosen signal space and indicate the decision boundaries formed by the optimum receiver.

2.

Compute the probability of error achieved by the optimum receiver.

3.

Define the average energy of this signal set as

$$E = \sum_{i} \sum_{j} E_{i,j} \pi_{i,j} ,$$

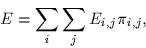
where E_i,j denotes the energy of signal s_i,j and 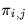$\pi_{i,j}$ denotes the corresponding a priori probabilities. Compute the average energy E.

4.

For a fixed value of the average energy E, how would you choose E_c and E_s so that the probability of error from part (b) is maximized? Explain.