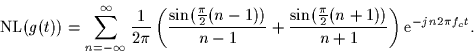![]()
![]()
![\begin{picture}
(385,80)(165,540)
\setlength {\unitlength}{0.009in}
%
\put(165...
...sebox{0pt}[0pt][0pt]{NL}}}
\put(405,575){\makebox(80,0)[t]{filter}}\end{picture}](img3.gif)
The nonlinear device NL is described by the relationship between its input x(t) and its output r(t) as
![]()
Assume the signal ![]() is passed through the above
nonlinearity. Sketch the resulting signal
is passed through the above
nonlinearity. Sketch the resulting signal ![]() and
show that this signal
can be represented as a Fourier series by
and
show that this signal
can be represented as a Fourier series by