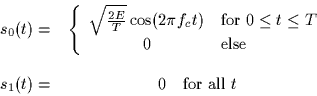
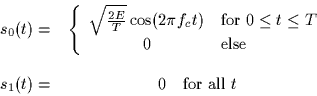
![\begin{picture}
(420,130)(200,540)
\setlength {\unitlength}{0.01in}
%
\thickl...
...{\makebox(0,0)[rb]{$\hat{b}$}}
\put(475,635){\makebox(0,0)[b]{$R$}}\end{picture}](img41.gif)
The gain of the amplifier is determineded by the control signal applied at the inputc (see diagram); if the control signal is positive the amplifier's gain is g > 0, otherwise the gain is -g.
Find the probability of error for this receiver as a function of the gain g.